Portfolio item number 10
The following limiting regimes were proven sufficient for a discrete local maximum principle, applicable for C-grid algorithms.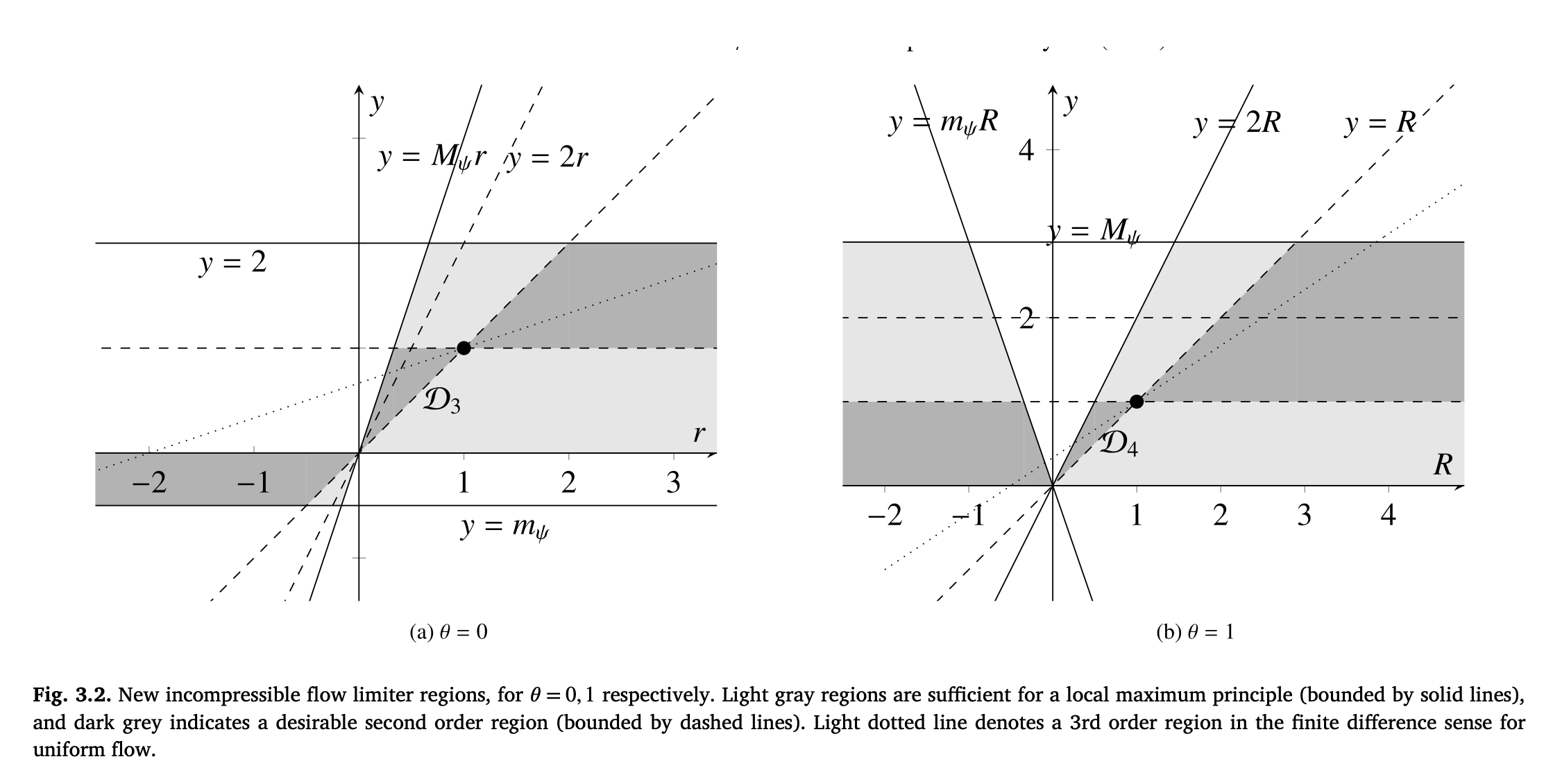 
Woodfield, J., Weller, H., & Cotter, C. J. (2024). New limiter regions for multidimensional flows. Journal of Computational Physics, 515(113286), 113286. https://doi.org/10.1016/j.jcp.2024.113286
Given a finite difference or finite volume scheme: \(\begin{aligned} u_{i,j}^{n+1} &= u_{i,j}^n - \Big[ F_{i+0.5}\left(u_i^R, u_{i+1}^L, c_{i+0.5}^n\right) - F_{i-0.5}\left(u_{i-1}^R, u_i^L, c_{i-0.5}^n\right) \Big]\\ & - \Big[ F_{j+0.5}\left(u_j^U, u_{j+1}^D, c_{j+0.5}^n\right) - F_{j-0.5}\left(u_{j-1}^U, u_j^D, c_{j-0.5}^n\right) \Big]. \end{aligned}\)
Where the superscripts $R,L,U,D$ denote the right, left, up, down subcell reconstructions of a cell centered at $(i,j)$. (For example $u^R_i$ denotes the reconstructed value of the solution at $(i+1/2,j)$, right of cell center $i,j$, and $u^L_{i+1}$ denotes the reconstructed value at $(i+1/2,j)$ left of cell center $(i+1,j)$.)
Reconstructions assume \(\theta = 0\) or \(\theta=1\) and one limits the slope
\[\begin{aligned} u_i^R &= u_i + \tfrac{\theta}{2} \, \psi(R_i) \, (u_i - u_{i-1}) + \tfrac{1-\theta}{2} \, \psi\!\left(\tfrac{1}{R_i}\right)(u_{i+1} - u_i), \\[3pt] u_i^L &= u_i + \tfrac{\theta}{2} \, \psi\!\left(\tfrac{1}{R_i}\right)(u_i - u_{i+1}) - \tfrac{1-\theta}{2} \, \psi(R_i)(u_i - u_{i-1}), \\[3pt] u_j^U &= u_j + \tfrac{\theta}{2} \, \psi(R_j)(u_j - u_{j-1}) + \tfrac{1-\theta}{2} \, \psi\!\left(\tfrac{1}{R_j}\right)(u_{j+1} - u_j), \\[3pt] u_j^D &= u_j + \tfrac{\theta}{2} \, \psi\!\left(\tfrac{1}{R_j}\right)(u_j - u_{j+1}) - \tfrac{1-\theta}{2} \, \psi(R_j)(u_j - u_{j-1}), \\[3pt] R_i &= \frac{u_{i+1}-u_i}{u_i - u_{i-1}}, \quad R_j = \frac{u_{j+1}-u_j}{u_j - u_{j-1}} . \end{aligned}\]Fluxes:
\[\begin{aligned} F\left(u_i^R, u_{i+1}^L, c_{i+0.5}\right) &= c_{i+0.5}^{+} u_i^R + c_{i+0.5}^{-} u_{i+1}^L, \\ F\left(u_{i-1}^R, u_i^L, c_{i-0.5}\right) &= c_{i-0.5}^{+} u_{i-1}^R + c_{i-0.5}^{-} u_i^L, \\ F\left(u_j^U, u_{j+1}^D, c_{j+0.5}\right) &= c_{j+0.5}^{+} u_j^U + c_{j+0.5}^{-} u_{j+1}^D, \\ F\left(u_{j-1}^U, u_j^D, c_{j-0.5}\right) &= c_{j-0.5}^{+} u_{j-1}^U + c_{j-0.5}^{-} u_j^D. \end{aligned}\]There are two limiter regions suitable for incompressible flow (depending on $\theta=0,1$). One can define new limiting functions $\psi$ in these regions, for new finite difference and finite volume methods.
Define your own limiter function using desmos: https://www.desmos.com/calculator/zxxr80vkyf